Call for participation

It is our pleasure to announce that the eleventh workshop Computational Logic and Applications (CLA 2018) will be held on 24-25 May 2018 in Paris, France. The workshop gathers researchers interested in quantitative aspects of mathematical logic and programming, including, but not limited, to topics such as:

  • combinatorics of lambda calculus and related formalisms,
  • quantitative aspects of program evaluation and normalization,
  • asymptotic enumeration and analytic methods in computational logic,
  • enumeration and random generation of formulae, terms and programs,
  • asymptotic analysis and random sampling of concurrency processes and beyond,
  • random software testing and counterexample generation including Monte Carlo techniques.

All researchers are cordially invited to attend.

Program committee

Important dates

  • Submission of talk proposals: 3 May 2018
  • Notification of acceptance: 5 May 2018
  • Registration deadline: 17 May 2018

Program

  Thursday, May 24th

  9:30-10:00 Breakfast

10:00-11:00 Michael Wallner
Asymptotic Enumeration of Compacted Binary Trees with Height Restrictions (slides)

When storing rooted trees it is useful to consider compression techniques. A simple idea is to store isomorphic subtrees only once and mark repeated occurrences with a pointer. A classical algorithm to establish such a compaction was analyzed by Flajolet, Sipala, and Steyaert. The resulting structure is called a compacted tree, being in fact no more a tree but a directed acyclic graph.

Our goal is the enumeration of such structures. Since the enumeration turns out to be extremely difficult, we restrict it to a sub problem by imposing a bound on the so-called right height. We solve this enumeration problem with the help of generating functions. Due to the superexponential growth of the counting sequence we use exponential generating function despite the fact that these objects are unlabeled. We first derive a calculus on exponential generating function capturing their recursive nature. This leads to a sequence of differential equations for the generating functions (also implying their D-finiteness) for which a singularity analysis is carried out.

This work is based on joint work with Antoine Genitrini, Bernhard Gittenberger, and Manuel Kauers.

  11:00-11:30 Coffee Break

11:30-12:30 Antoine Genitrini
Compacted Binary Trees: A preliminary work on Implication Boolean expressions represented as Directed Acyclic Graphs (slides)

The nature of tautologies in the context of Boolean Implication trees has been first studied by Moczurad, Tyszkiewicz and Zaionc. Their model was based on the classical Catalan tree model decorated with the connective Implication and with variables. Then several papers dealt with the same model in order to obtain quantitative results for the shape of a typical tautology. We here present the model of Compacted Binary Trees that are in fact Directed Acyclic Graphs (DAGs) and we present the first quantitative results and a recursive random generator (in fact an unranking algorithm) for this model of Boolean DAGs.

  12:30-14:30 Lunch Break

14:30-15:30 Isabella Larcher
On the number of variables in special classes of random lambda-terms (slides)

We investigate the number of variables in two special subclasses of lambda-terms that are restricted by a bound of the number of abstractions between a variable and its binding lambda, and by a bound of the nesting levels of abstractions, respectively. These restrictions are on the one hand very natural from a practical point of view, and on the other hand they simplify the counting problem compared to that of unrestricted lambda-terms in such a way that the common methods of analytic combinatorics are applicable. We will show that the total number of variables is asymptotically normally distributed for both subclasses of lambda-terms with mean and variance asymptotically equal to $C_1 n$ and $C_2 n$, respectively, where the constants $C_1$ and $C_2$ depend on the bound that has been imposed. So far we just derived closed formulas for the constants in case of the class of lambda-terms with a bounded number of abstractions between each variable and its binding lambda. However, for the other class of lambda-terms that we consider, namely lambda-terms with a bounded number of nesting levels of abstractions, we investigate the number of variables in the different abstraction levels and thereby exhibit very interesting results concerning the distribution of the variables within those lambda-terms.

  15:30-15:45 Coffee Break

15:45-16:45 Sergey Dovgal
Statistical properties of lambda terms (slides)

We consider plain and closed lambda terms sampled uniformly at random and investigate the distribution of several parameters inside them. For the number of variables, abstractions, successors and redexes we obtain normal limit laws (for both, plain and closed lambda terms). For several other parameters (index distribution, redex search time, number of head abstractions, number of free variables) we obtain discrete limit laws. Next, for height profile with different height notions we obtain Rayleigh distribution. In addition, we present several conjectures motivated by empirical evidence. Our tools comprise analytic combinatorics and transfer theorems for infinite systems of functional equations.

Joint work with Maciej Bendkowski and Olivier Bodini.

16:45-17:30 Jean Peyen
On some linear lambda term parameters (slides)

The asymptotic analysis of linear lambda-terms can be done in a very fine way thanks to the bijection with trivaluate maps described by Bodini-Gardy-Jacquot. We are now interested in the analysis of some important parameters. We will show in this talk that the number of free variables is asymptotically Gaussian with mean in $(2n)^{1/3}$. We will also present the work in progress on other parameters.

Joint work with Olivier Bodini.

  17:30-19:00 Workshop Meeting

  Friday, May 25th

  9:00-9:15 Breakfast

9:15-10:15 Noam Zeilberger
A sequent calculus for a semi-associative law (slides)

We introduce a sequent calculus with a simple restriction of Lambek's product rules that precisely captures the classical Tamari order, i.e., the partial order on fully-bracketed words (equivalently, binary trees) induced by a semi-associative law (equivalently, right rotation). We establish a focusing property for this sequent calculus (a strengthening of cut-elimination), which yields the following coherence theorem: every valid entailment in the Tamari order has exactly one focused derivation. We then describe two main applications of the coherence theorem, including: 1. A new proof of the lattice property for the Tamari order, and 2. A new proof of the Tutte-Chapoton formula for the number of intervals in the Tamari lattice $Y_n$.

This is based on the extended version of an article presented at FSCD 2017: https://arxiv.org/abs/1803.10080.

  10:15-10:30 Coffee Break

10:30-11:30 Catherine Dubois and Alain Giorgetti
Lambda terms and maps, formally (II) (slides)

At first glance lambda calculus and theory of maps (graphs embedded on a surface) seem to be two disjointed research domains. However several bijections between families of lambda terms and maps have been recently established. With the Coq proof assistant we try to mechanize a demonstration that these correspondences are bijective. In this talk we show how this research has led us to new representations of these objects. As this work is in progress we use random generators (using QuickCheck developed by Pierce et al.) to check lemmas before proving them.

11:30-12:30 Maciej Bendkowski
Combinatorics of explicit substitutions (slides)

$\lambda\upsilon$ is an extension of the $\lambda$-calculus which internalises the calculus of substitutions. We investigate the combinatorial properties of $\lambda\upsilon$ focusing on the quantitative aspects of substitution resolution. Remarkably, an unexpected correspondence between the counting sequence for $\lambda\upsilon$-terms and famous Catalan numbers is exhibited. As a by-product, we establish effective sampling schemes for random $\lambda\upsilon$-terms. We show that typical $\lambda\upsilon$-terms represent, in a strong sense, non-strict computations in the classic $\lambda$-calculus. Moreover, typically almost all substitutions are in fact suspended, i.e. unevaluated, under closures. Consequently, we argue that $\lambda\upsilon$ is an intrinsically non-strict calculus of explicit substitutions. Finally, we investigate the distribution of various redexes governing the substitution resolution in $\lambda\upsilon$ and investigate the quantitative contribution of various substitution primitives.

Joint work with Pierre Lescanne.

  12:30-14:30 Lunch Break

14:30-15:30 Pierre Lescanne
Counting Environments and Closures (slides)

Environments and closures are two of the main ingredients of evaluation in $\lambda$-calculus. A closure is a pair consisting of a $\lambda$-term and an environment, whereas an environment is a list of $\lambda$-terms assigned to free variables. We investigate some dynamic aspects of evaluation in $\lambda$-calculus considering the quantitative, combinatorial properties of environments and closures. Focusing on two classes of environments and closures, namely the so-called plain and closed ones, we consider the problem of their asymptotic counting and effective random generation. We provide an asymptotic approximation of the number of both plain environments and closures of size $n$. Using the associated generating functions, we construct effective samplers for both classes of combinatorial structures. Finally, we discuss the related problem of asymptotic counting and random generation of closed environments and closures.

Joint work with Maciej Bendkowski.

  15:30-16:00 Coffee Break

16:00-17:00 Paul Tarau
Combinatorial Testing Techniques for Intuitionistic Propositional Theorem Provers (slides)

Proving a theorem in intuitionistic propositional logic, with implication as its only primitive, is known as one of the simplest to state PSPACE-complete problem. At the same time, via the Curry-Howard isomorphism, it is the key to finding a lambda term that inhabits a given type, if it exists. However, as a significant number of papers, all starting with Gentzen's LJ calculus can witness it, conceptual simplicity has not come in this case with comparable computational counterparts, facing challenges related not only to soundness and completeness but also to termination and scalability problems. Can a simple solution, in the tradition of "lean theorem provers" be uncovered that matches the conceptual simplicity of the problem, while being able to handle randomly generated large formulas? Could such a theorem prover be used to produce random simply typed lambda terms comparable in size with Boltzmann samplers? In search for an answer, working on the two sides of the Curry-Howard isomorphism, we develop a combinatorial testing framework, involving all-term and random term generators, covering both simply-typed lambda terms in normal form and implicational formulas. With its help, we derive a sequence of minimalistic theorem provers, via declarative program transformations steps, while working through some unexpected challenges and highlighting connections to subtleties of type inference mechanisms for the simply typed lambda calculus. We use our combinatorial tester to cover soundness, completeness and termination properties as well as scalability to large formulas and progressively improved performance. We chose Prolog as our meta-language. Being derived from essentially the same formalisms as those we are covering reduces the semantic gap and results in a surprisingly concise and efficient declarative implementation.

Our implementation is available at https://github.com/ptarau/TypesAndProofs.

17:00-18:00 Maciej Bendkowski
Polynomial tuning of multiparametric combinatorial samplers (slides)

Boltzmann samplers and the recursive method are prominent algorithmic frameworks for the approximate-size and exact-size random generation of large combinatorial structures, such as maps, tilings, RNA sequences or various treelike structures. In their multiparametric variants, these samplers allow to control the profile of expected values corresponding to multiple combinatorial parameters. One can control, for instance, the number of leaves, profile of node degrees in trees or the number of certain subpatterns in strings. However, such a flexible control requires an additional nontrivial tuning procedure. We propose an efficient polynomial-time, with respect to the number of tuned parameters, tuning algorithm based on convex optimisation techniques. We illustrate the efficiency of our approach using several applications of rational, algebraic and Pólya structures including polyomino tilings with prescribed tile frequencies, planar trees with a given specific node degree distribution, and weighted partitions.

Joint work with Olivier Bodini and Sergey Dovgal.

  19:30- Social Dinner

Registration

The registration for CLA 2018 is now open! Participation is free of charge! We invite the participants to give talks of 45 minutes on topics relevant to the theme of the workshop. Please indicate your interest in giving a talk by sending an email to

(λx.x@lip6.fr)cla

including

  • your current affiliation,
  • the title of your talk(*), and
  • an abstract of about 200 words(*).

Following a selection process during the period of 3--4 May 2018, accepted talks will be announced on May 5 2018.

(*) If you don't plan to give a talk, please indicate it in the email.

Venue

The worshop will be held at the Sorbonne University (ex UPMC), Campus Pierre et Marie Curie (metro Jussieu).

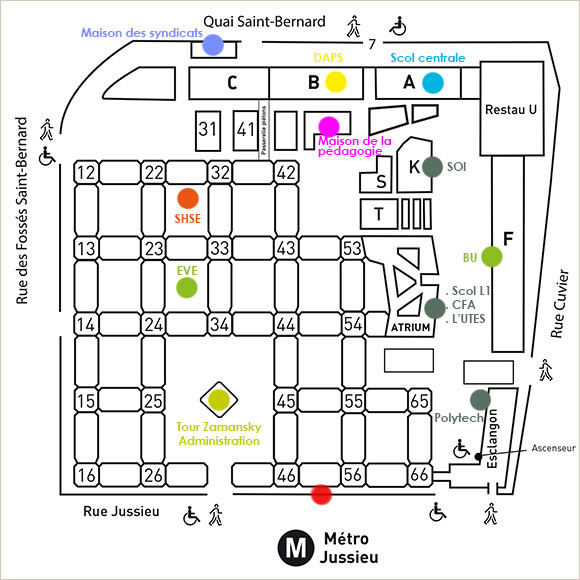
On the map of the Campus Pierre et Marie Curie (metro Jussieu). There is a single entry on the campus, just near Jussieu Metro station. The entry is between the towers 46 and 56 (the red point).

ROOM UPDATE

Reach the tower 14 (15 is also fine). Then, take the evelator to the 5th floor. The corridor 14/15 is open and there you will find the room 507.

Participants

  • Cyril Banderier (Université Paris Nord)
  • Maciej Bendkowski (Jagiellonian University)
  • Olivier Bodini (Université Paris Nord)
  • Julien Clément (CNRS, GREYC, Caen)
  • Sergey Dovgal (Université Paris Nord)
  • Catherine Dubois (Ecole Nationale Supérieure d'Informatique pour l'Industrie et l'Entreprise)
  • Zeinab Galal (Université Paris Diderot)
  • Danièle Gardy (Université de Versailles-Saint-Quentin-en-Yvelines)
  • Antoine Genitrini (Sorbonne Université)
  • Stefano Guerrini (Université Paris Nord)
  • Alain Giorgetti (Université Bourgogne Franche-Comté)
  • Bernhard Gittenberger (Technische Universität Wien)
  • Katarzyna Grygiel (Jagiellonian University)
  • Isabella Larcher (Technische Universität Wien)
  • Pierre Lescanne (ENS Lyon)
  • Florian Luca (University of the Witwatersrand)
  • Philippe Marchal (Université Paris Nord)
  • Mehdi Naima (Université Paris Nord)
  • Le Thanh Dung Nguyen (École Normale Supérieure de Paris & Université Paris 13)
  • Martin Pépin (Sorbonne Université)
  • Jean Peyen (University of Leeds)
  • Paul Tarau (University of North Texas)
  • Michael Wallner (Université de Bordeaux)
  • Marek Zaionc (Jagiellonian University)
  • Noam Zeilberger (University of Birmingham)

History

Below you can find details regarding some of the most recent CLA editions:

Contact

CLA 2018 is organized jointly by Laboratoire d'Informatique de Paris-Nord and Laboratoire d'Informatique de Paris 6.

Main organizers are: